In the realm of computer science and software development, the efficiency of data processing is paramount. One fundamental question that often arises is: Why is processing a sorted array faster than processing an unsorted array? Understanding this concept is crucial for optimizing algorithms and improving application performance.
This article delves into the reasons behind the performance disparity between sorted and unsorted arrays, exploring aspects like algorithm efficiency, memory access patterns, and CPU optimizations.
Algorithm Efficiency: The Power of Sorted Data

Binary Search vs. Linear Search
One of the most significant advantages of sorted arrays is the ability to utilize more efficient search algorithms. For instance, binary search can be employed on sorted arrays, operating in O(log n) time complexity. In contrast, searching through an unsorted array typically requires linear search, which operates in O(n) time complexity.
Example:
int binarySearch(int arr[], int size, int target) {
int low = 0, high = size - 1;
while (low <= high) {
int mid = low + (high - low) / 2;
if (arr[mid] == target) return mid;
else if (arr[mid] < target) low = mid + 1;
else high = mid - 1;
}
return -1; // Element not found
}
In this example, the binary search algorithm efficiently locates the target element in a sorted array. Attempting the same on an unsorted array would necessitate a linear search, which is less efficient.
Sorting Algorithms: Optimized for Sorted Data
Certain sorting algorithms, such as insertion sort, perform significantly better on nearly sorted data. When the data is already sorted or nearly sorted, these algorithms can operate in O(n) time, compared to O(n²) in the worst case for unsorted data.
Example:
void insertionSort(int arr[], int size) {
for (int i = 1; i < size; ++i) {
int key = arr[i];
int j = i - 1;
while (j >= 0 && arr[j] > key) {
arr[j + 1] = arr[j];
--j;
}
arr[j + 1] = key;
}
}
This algorithm efficiently sorts an array that is nearly sorted. However, its performance diminishes with unsorted data.
Memory Access Patterns: Cache Efficiency
Data Locality and Cache Misses
Modern CPUs retrieve data in contiguous blocks known as cache lines, typically around 64 bytes. Sorted arrays tend to have better data locality, meaning that adjacent elements are stored close together in memory. This arrangement increases the likelihood that the required data is already in the cache, reducing memory access times.
In contrast, unsorted arrays often result in more random access patterns, causing frequent cache misses. Each cache miss forces the CPU to fetch data from the main memory, which is significantly slower than accessing it from the cache. This leads to higher processing times.
Example:
for (int i = 0; i < size; ++i) {
process(sortedArray[i]); // Higher cache locality
}
for (int i = 0; i < size; ++i) {
process(unsortedArray[i]); // More random access
}
In the first loop, accessing elements in a sorted array improves cache efficiency. In the second loop, accessing elements in an unsorted array may cause more cache misses, leading to slower performance.
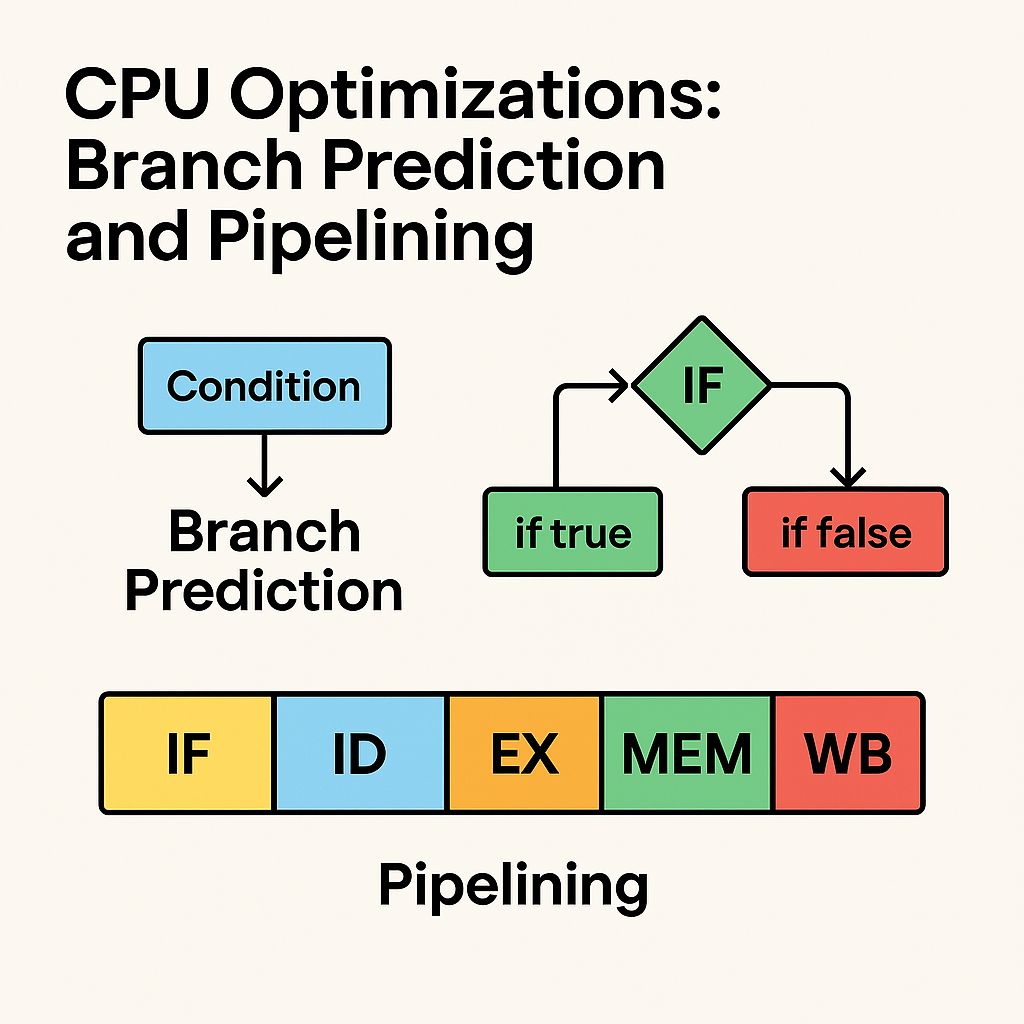
CPU Optimizations: Branch Prediction and Pipelining
Predictable Branching
Modern CPUs use branch prediction to guess the outcome of conditional operations, allowing for more efficient instruction execution. Sorted arrays exhibit a predictable pattern because the data is arranged in order. This predictability enables the CPU to make accurate branch predictions, reducing the likelihood of costly mispredictions.
Example:
for (int i = 1; i < size; ++i) {
if (sortedArray[i] != sortedArray[i - 1]) {
process(sortedArray[i]);
}
}In this loop, the condition is more likely to be true, leading to predictable branching. This predictability enhances CPU performance.
Efficient Pipelining
Processor pipelining allows for overlapping the execution of multiple instructions, increasing throughput. Sorted arrays contribute to this optimization by offering an anticipated and consistent progression of ascending or descending values. This coherence aids the CPU's branch predictor in making more accurate projections, ultimately leading to fewer pipeline stalls attributed to mispredicted branches.
Example:
for (int i = 0; i < size; ++i) {
process(sortedArray[i]);
}
In this loop, the consistent pattern of sorted data facilitates efficient pipelining, enhancing overall performance.
Practical Implications: Real-World Applications
Search Operations
Utilizing binary search on sorted arrays significantly reduces search times compared to linear search on unsorted arrays. This improvement is particularly beneficial in applications requiring frequent data retrieval, such as databases and search engines.
Sorting Algorithms
Algorithms like merge sort and quicksort perform more efficiently on sorted data, reducing the overall computational complexity and enhancing performance in applications involving large datasets.
Data Processing Pipelines
In data processing pipelines, sorting data beforehand can lead to more efficient processing, reducing the time and resources required for tasks like filtering, aggregation, and transformation.
When Sorting Is Worth the Overhead
You might wonder: if sorting data improves processing, why not always sort?
Great question. The answer lies in trade-offs:
Sorting itself takes time (at least O(n log n) for efficient algorithms).
If the array is only used once and performance is acceptable, sorting may be unnecessary.
But for repeated operations (like multiple searches or data processing loops), sorting once and processing many times is vastly more efficient.
A sorted structure pays off best when:
The array is large.
Multiple queries or scans are expected.
Memory access time is critical (e.g., in low-latency systems).
Frequently Asked Questions (FAQs)
1. Why is a sorted array faster to process than an unsorted array?
Answer:
Processing a sorted array is faster because it allows for more efficient algorithms like binary search (O(log n)) instead of linear search (O(n)). Additionally, sorted arrays benefit from better CPU cache locality and branch prediction, which reduces latency during memory access and improves instruction execution speed.
2. How does sorting improve search operations in arrays?
Answer:
When an array is sorted, you can use binary search, which drastically reduces the number of comparisons needed to find an element. This leads to faster search times, especially in large datasets. Unsorted arrays, in contrast, require checking each element one-by-one (linear search), which takes longer.
3. Does sorting improve performance for all types of algorithms?
Answer:
No, not all algorithms benefit equally. However, many algorithms—especially those related to searching, filtering, and merging—perform significantly better when the data is sorted. Sorting is particularly beneficial in repetitive or high-volume operations where the sorting cost is offset by long-term speed gains.
4. Why do sorted arrays improve CPU cache performance?
Answer:
Sorted arrays often result in sequential memory access. This enhances spatial locality, which means the CPU can load multiple useful values into the cache in a single operation. As a result, there's a higher cache hit rate and fewer slow accesses to main memory.
5. How does branch prediction relate to sorted arrays?
Answer:
In sorted arrays, control flow becomes more predictable (e.g., loops with simple conditions). This allows the CPU’s branch predictor to more accurately guess the next steps in execution. With unsorted arrays, unpredictable branches can lead to CPU pipeline stalls, reducing performance.
6. Can sorting an array actually save time later in a program?
Answer:
Yes. While sorting has an upfront cost (usually O(n log n)), it often saves time during repeated operations like searching, filtering, or deduplication. If the array is accessed multiple times, the long-term performance benefits of having sorted data outweigh the initial cost.
7. What sorting algorithm works best when data is almost sorted?
Answer:
Insertion Sort performs exceptionally well on nearly sorted data. Its best-case time complexity is O(n), and it adapts quickly with minimal comparisons and swaps. This makes it ideal for situations where data is mostly—but not entirely—sorted.
8. Are sorted arrays used in real-world systems like databases?
Answer:
Absolutely. Databases rely heavily on sorted data structures like B-trees and indexes to optimize read operations. Sorting allows databases to execute fast range queries, reduce I/O overhead, and provide real-time search results more efficiently.
9. Should I always sort an array before processing it?
Answer:
Not always. If the array is used only once and for simple operations, sorting may add unnecessary overhead. But for applications involving frequent searches, comparisons, or batch operations, sorting once can significantly improve performance throughout the system.
10. Is it better to sort during input or before processing?
Answer:
Sorting during input can be highly efficient, especially in streaming data or logging systems. By maintaining order early, you eliminate the need for full-array sorting later, allowing for continuous, fast processing as new data comes in.
Discover more from 9Mood
Subscribe to get the latest posts sent to your email.





















0 Comments